Projection

There are two types of projections: a vector projection and an orthogonal (i.e., plane) projection.

Vector Projection: Given two vectors

\vec{a}

and

\vec{b}

in the same

n

-dimensional vector space, the vector projection

{𝖯𝗋𝗈𝗃}_{\vec{b}} (\vec{a})

measures the component of

\vec{a}

in the direction of

\vec{b}

(i.e., the part of

\vec{a}

that is parallel to

\vec{b}

). In the example of Figure 3a,

\vec{a}

’s projection on

\vec{b}

{\vec{a}}_{1}

, where the length of

{\vec{a}}_{1}

is geometrically

| | a_{1} | | = | | a | | \cos 𝜃 = | | a | | \frac{a \cdot b}{| | a | | \cdot | | b | |} = \frac{a \cdot b}{| | b | |}

. Let

\vec{b^{'}}

be a unit vector of

\vec{b}

, that is

\vec{b^{'}} = \frac{\vec{b}}{| | b | |}

. Then,

{\vec{a}}_{1} = | | a_{1} | | \cdot \vec{b^{'}} = \frac{a \cdot b}{| | b | |} \cdot \frac{\vec{b}}{| | b | |} = \frac{a \cdot b}{| | b | |^{2}} \vec{b}

. Thus,

{𝖯𝗋𝗈𝗃}_{\vec{b}} (\vec{a}) = \frac{a \cdot b}{| | b | |^{2}} \vec{b}

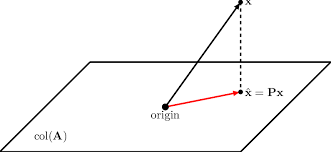
Orthogonal Projection: Given the vector

\vec{x}

and a set of mutually orthogonal vectors

{\vec{p}}_{0}, {\vec{p}}_{1}, \dots, {\vec{p}}_{n - 1}

that span the subspace

P

, the orthogonal projection

{𝖯𝗋𝗈𝗃}_{P} (\vec{x})

measures how much of

\vec{x}

lies in

P

(i.e., the component of

\vec{x}

within

P

). In the example,

\vec{x}

’s projection onto

P

(red arrow) equals the sum of the projections of

\vec{x}

onto each orthogonal basis vector

{\vec{p}}_{i}

spanning

P

{𝖯𝗋𝗈𝗃}_{P} (\vec{x}) = \sum_{i = 0}^{n - 1} {𝖯𝗋𝗈𝗃}_{{\vec{p}}_{i}} (\vec{x})

. This computation can be viewed as expressing

\vec{x}

in a coordinate system defined by the

n

orthogonal vectors.

$⟨$ Definition A-10.4 $⟩$ Vector and Orthogonal Projections

Vector Projection: Given two vectors $\vec{a}$ and $\vec{b}$ in the same vector space, the vector projection of $\vec{a}$ on $\vec{b}$ is:
${𝖯𝗋𝗈𝗃}_{\vec{b}} (\vec{a}) = {\vec{a}}_{p} = \frac{\vec{a} \cdot \vec{b}}{| | b | |^{2}} \vec{b}$ $▹$ where $| | {\vec{a}}_{p} | | = | | \vec{a} | | \cos 𝜃$
Orthogonal Basis: If the $n$ -dimensional plane (or subspace) $P$ is spanned by the mutually orthogonal $n$ -dimensional vectors ${\vec{p}}_{0}, {\vec{p}}_{1}, \dots, {\vec{p}}_{n - 1}$ ,
then the matrix $P = [\begin{matrix} {\vec{p}}_{0} \\ {\vec{p}}_{1} \\ ⋮ \\ {\vec{p}}_{n - 1} \end{matrix}]$ is defined to be an orthogonal basis of plane $P$ .
Orthogonal Projection: Given the orthogonal basis matrix $P = [\begin{matrix} {\vec{p}}_{0} \\ {\vec{p}}_{1} \\ ⋮ \\ {\vec{p}}_{n - 1} \end{matrix}]$ ,
vector $\vec{a}$ ’s orthogonal projection on $P$ is:
${𝖯𝗋𝗈𝗃}_{P} (\vec{a}) = \sum_{i = 0}^{n - 1} {𝖯𝗋𝗈𝗃}_{{\vec{p}}_{i}} (\vec{a})$

Based on the definition of orthogonal projection, the following properties are derived:

Orthogonal Basis: In an

n

-dimensional vector space, any mutually orthogonal

n

vectors in the vector space span the subspace

P

that is identical to the entire vector space. Further, the orthogonal projection of any vector in the vector space on

P

is guaranteed to be a unique vector.

Non-orthogonal Basis: In an

n

-dimensional vector space, suppose some

n

non-orthogonal vectors satisfy the following two conditions: (i) they span the entire vector space; (ii) they are linearly independent (i.e., one vector cannot be expressed as a linear combination of the other vectors). Then, the

n \times n

matrix

P

comprised of these

n

vectors forms a basis for the entire vector space

V

, and the matrix-to-vector multiplication

P \vec{v}

for each

\vec{v}

in the vector space is guaranteed to yield a unique vector. However, the formula

{𝖯𝗋𝗈𝗃}_{P} (\vec{v})

is not a valid geometric projection of the vector

\vec{v}

P

, because the

n

basis vectors are non-orthogonal. Yet, the computation of

P \vec{v}

can be thought of as uniquely transforming

\vec{v}

into a different coordinate system that expresses the vector space with respect to

n

non-orthogonal vectors in

P

$⟨$ Theorem A-10.4 $⟩$ Uniqueness of Transformed Vectors

Orthogonal Basis: If some $n$ vectors are a orthogonal basis of the plane $P$ in the $n$ -dimensional vector space, then $P$ is the same as the entire vector space, and ${𝖯𝗋𝗈𝗃}_{P} (v)$ for every vector $\vec{v}$ in the vector space is guaranteed to be a unique vector.
Non-orthogonal Basis: If some $n$ vectors are a non-orthogonal basis of the plane $P$ in the $n$ -dimensional vector space (i.e., each vector is linearly independent and they span $P$ ), then $P$ is the same as the entire vector space, and $P \vec{v}$ is guaranteed to result in a unique vector.

A-10.4 Projection